Deep Learning study
Improved Precision and Recall Metric for Assessing Generative Models ( GAN metric ) 본문
Improved Precision and Recall Metric for Assessing Generative Models ( GAN metric )
HwaniL.choi 2022. 2. 13. 16:41
생성 된 이미지를 평가할 때는 두 가지를 고려해 평가한다고 생각할 수 있습니다.
Fidelity : 얼마나 실제같은 이미지를 생성하는가.
Diversity : GAN이 얼마나 다양한 이미지를 생성하는가.
하지만 GAN 을 평가할 때 가장 많이 쓰이는 FID score 는 단순 두 분포의 거리를 측정하는 방법이기 때문에, 각각에 대한지표를 알 수 없다는 단점이 있습니다. 이렇게 조금은 애매한 지표이지만 그렇다고 GAN이 생성하는 이미지들의 quality를 측정할 마땅한 다른 방법이 딱히 없기에 가장 널리 쓰이고 있죠.
Improved Precision and Recall Metric for Assessing Generative Models
(GAN 을 평가지표로 Precision 과 Recall 을 처음 소개한 논문은 아니지만, 뒤에나올 논문과 비교하기 위해서 이논문을 소개합니다.)
이 논문에서는 Precision, Recall 을 소개합니다.
precision, recall 이라고하면 일반적으로 '정밀도, 재현율' 라고 알고있는 분류성능평가지표 입니다.
precision은 모델 기준에서, 모델이 True라고 한 것 중에 실제 True의 비율이고, recall 은 실제 데이터 기준에서 True 인 것 중 모델이 True라고 판별한 것 입니다.
결론부터 말하자면 Precision은 Fidelity의 지표이고, Recall 은 Diversity의 지표입니다. 왜 각각이 fideility와 diversity를 의미하는지 위의 의미를 생각하면서 아래 그림을 같이 보겠습니다.

$P_r$ 은 Real 의 분포이고 $P_g$ 는 Fake의 분포입니다.
Precision (Fidelity)
여기서의 precision 의 이미는 그림 (b) 를 원래의 precision 의미와 빗대어 생각해보면 쉽게 알 수 있습니다. Precision은 $P_r$ 에 얼마나 많은 Fake sample들이 들어가냐 입니다.
다시 말해서 생성된 이미지들 중에서 (모델이 True 라고 한 것) 실제로 $P_r$에 들어간 것(실제 True 인 것) 입니다.
Fake sample 들이 Real 분포 안에 존재한다면, 그만큼 실제와 같은 생성 들 이겠죠. 그래서 이 precision이 높을 수록 GAN은 Fidelity가 높은 이미지를 많이 생성한다고 할 수 있겠습니다.
Recall (Diversity)
precision 과 비슷하게, (c) 를 본다면 쉽게 알 수 있습니다.
$P_g$에 얼마나 많은 Real sample 들이 들어가느냐입니다. 다시말해서 실제 이미지들 중에서 ( 실제 True 인 것 중에서) $P_g$ 에 들어간 것 입니다.
즉, $P_g$ 가 $P_r$ 을 얼마나 잘 커버 했냐 라고 생각한다면, real 분포의 넓은 부분을 커버 할 수록 다양한 sample 들 까지 생성할 수 있겠죠. 그래서 Recall 은 Diversity에 대한 지표입니다.
그럼 여기서 자연스럽게 의문이 하나 생깁니다.
그래서 의미는 알겠는데, $P_r$ 과 $P_g$ 는 어떻게 알 수 있을까.
정확히 말하자면 당연히 알 수 없습니다. 하지만 같은 방법으로 같은 어떤 다른 공간으로 mapping 또는 embedding을 한 뒤 두 분포의 상대적인 위치를 파악하고 근사할 수 는 있습니다. RGB 공간은 차원이 너무크고 다루기 힘들기때문에 embedding을 이용하는 것은 이젠 지극히 자연스러우며 이젠 보편적인 방법입니다 (일 겁니다 .. ?).
여기서는 VGG16 을 이용해 각 sample 당 4096 dimension으로 embedding 합니다. 이제 모든 real, fake sample 들이 embedding space (feature space) 에 있기 때문에 다루기는 훨씬 쉬워졌지만, 여기서 분포를 수치적으로 근사하는것은 여전히 어려운 일입니다. 그래서 좀 더 간단한 근사할 수 있는 방법을 소개합니다.
간단하게도 k-Nearest Neighborhood 알고리즘을 사용해서 각 real 과 fake 의 manifold를 근사합니다.

위의 그림을 보면 직관적으로 쉽게 알 수 있습니다. 각 sample 들을 기준으로 kNN ball 을 만들어 manifold를 근사하는 방식입니다.
그럼 각 $P_r, P_g$ 를 근사하는 방법을 알았으니, 수식으로 어떻게 precision 과 recall을 계산하는지 알아봅시다.
$$ f(\phi, \Phi) = \begin{cases} 1, & \mbox{ if } \lVert \phi - \phi ' \rVert_2 \le \lVert \phi ' - NN_k(\phi ' , \Phi) \rVert_2 \mbox{ for at leat one } \phi' \in \Phi \\ 0, & \mbox{ otherwise, } \end{cases} $$
$\Phi$ 는 real 또는 fake 의 embedding vector(feature vector) 들의 set 이고(각각 $\Phi_r$,$\Phi_g$) $NN_k(\phi', \Phi) 는 $\phi'$ 에서 $k$ 번째로 가까운 feature vector 를 계산해줍니다.
$ f(\phi, \Phi) $ 로 각 sample 이 어떤 manifold 안에 들어가냐 들어가지 않느냐를 알 수 있습니다. 1이 될 조건을 보면 inequality 오른쪽의 식은 , $\phi'$ 와 이것과 $k$ 번째 가까운 것과의 거리(r) 입니다. 즉 $\phi'$ 를 중심으로 r 의 반지름을 가지는 Ball 입니다. 편하게 위의 그림대로 하나의 원을 생각하시면 되겠습니다 (좀 더 정확히 말하자면 hypersphere 입니다). 그리고 inequality 의 왼쪽의 식을 보면 대상이 되는 $\phi$ 와 set $\Phi$ 에 있는 어떤 $\phi'$ 과의 거리입니다.
적어도 하나의 $\phi'$ 에 대해서 만족한다는 것은 ,쉽게 말하자면 $\Phi$ 로 근사시킨 manifold 에 들어간다는 의미입니다.
그래서 하나의 indicator fucntion 역할을 하는것입니다.
어떤 $\phi$가 $\Phi$ 의 manifold 안에 존재하냐 안하냐를 판단해주는 함수인거죠.
그럼 이제 Precision 과 Recall 을 수치적으로 정의할 수 있습니다.
$$\text{precision}(\Phi_r, \Phi_g) = {1 \over |\Phi|} \sum_{\phi_g \in \Phi_g} f(\phi_g , \Phi_r) \\ \text{recall}(\Phi_r, \Phi_g) = {1 \over |\Phi_r|}\sum_{\phi_r \in \Phi_r} f(\phi_r, \Phi_g)$$

수식도 위의 의미만 다시 생각해본다면 상당히 직관적으로 이해할 수 있지만, 조금 더 이해하기 쉽도록 PPT로 제가 그린 그림입니다.
Precision&Recall of StyleGAN
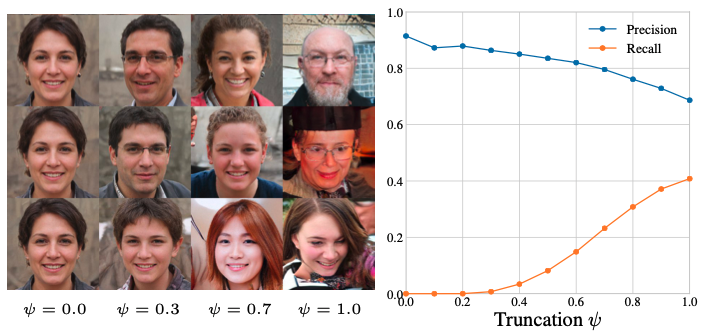
먼저 위의 그림을 이해하기 위해서는 Truncation method 에 대해서 알아야하는데, Truncation을 많이 할 수록 GAN이 만들어내는 평균적인 모습에 가까워진다고 생각하시면 되겠습니다. 당연히 StyleGAN 저자도 언급했지만 , Truncation은 생성 이미지의 diversity를 희생하고 품질(fidelity)를 택하는 방법인것이죠. 0 이 최대로 truncation 한 것, 1이 truncation이 적용되지 않은 상태 입니다. (StyleGAN1,2,3 에 대한 포스팅은 나중에 하겠습니다. )
그럼 truncation을 많이 할 수록 diversity는 낮아지지만 fidelity가 높아지므로, precision은 높아지고 recall 은 낮아져야되겠습니다. 오른쪽 그래프를 보시면 그 결과를 확인 할 수 있고, 실제로 precision 과 recall 이 원했던 방향의 성능지표로 활욜 할 수 있음을 보여줍니다.
* 이건 단지 Truncation 방법의 문제만은 아닙니다. 생성모델의 diversity가 높아지면 fidelity가 낮아지고 fidelity가 높아지게 만들면 diversity가 줄어드는것은 고질적인 문제입니다.
Estimating the quality of individual samples
FID도 마찬가지지만, 앞에서 봐왔듯이 Precision, Recall 모두 분포에대한 성능 지표입니다. 다시말해서 sample 1장에 대한 점수를 메길 수 있는 방법은 아닙니다. (real manifold에 들어왔는지 아닌지는 판별할 수 있지만..)
그래서 여기서 sample 당 점수를 메기는 방법 하나를 소개합니다.
Realism Score
생성 된 개별 샘플에 대한 metric 입니다.
$$R(\phi_g, \Phi_r) = \max_{\phi_r} \left\{ {\lVert \phi_r - NN_k(\phi_r, \Phi_r) \rVert_2 \over \lVert \phi_g - \phi_r \rVert_2 } \right\}$$
의미적으로 생각하면 어떤 real ball 안에 들어왔다면, 그 real sample과 가까울 수록 점수가 높다는 것이고, real manifold에 들어오지 못했다면, 그 거리만큼 점수가 낮아지는 것 이죠. 여튼 real manifold에 들어가면 1 이상의 값, 들어가지 않으면 1 이하의 값이 나옵니다.
그래서 이 Realism Score 로 생성된 이미지들의 각각 점수를 부여해서 순위를 메길 수 있는겨쥬.

여튼 설명은 여기까지 입니다. 원래 precision & recall 을 개선한 Density & Coverage 논문도 같이 쓰려했는데 생각보다 길어져서 나중에 .. 언젠가 다시 오겠습니다.
Reference
[1] Improved Precision and Recall Metric for Assessing Generative Models




